بحث علمي عن قاعدة كرامر
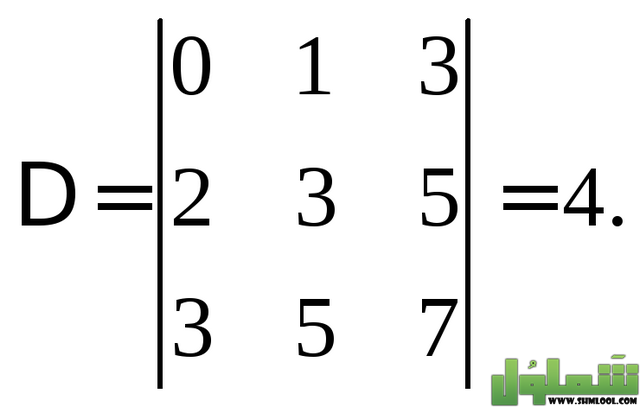
بحث علمي عن قاعدة كرامر، يعتبر كرامر من العلماء المشهورة في مجال الرياضيات، فهو ولد سنة 1704 ميلادياً وتوفي سنة 1752، وظهرت عبقريته في الرياضيات من سن مبكر، واستطاع أن يحصل على الدكتوراه وهو في الثامنة عشر من عمره، وهو في سن العشرين عين رئيس مشارك في الرياضيات بجامعة جينيف.
مقدمة بحث عن قاعدة كرامر
تزايد البحث كثيراً عن هذه القاعدة لأن القواعد والنظريات من أهم الأشياء التي تميزت بها الرياضيات، تعتبر من القواعد المبرهنة بالجبر الخطي التي تساعد على منح الحلول لعدد من المعادلات الجبرية الخطية، وعرفت هذه القاعدة بهذا الاسم نسبة إلى مكتشفها غابريال كرامر، ولكنه يكون من النادر الاعتماد عليها واستخدامها في التطبيقات التي تضم مجموعة من المعادلات.
استخدام قاعدة كرامر في حال المعادلات الخطية

- تساعد القاعدة على إعطاء الإثباتات والبراهين التي تستخدم في حل المعادلات الخطية، وهذا من خلال الاعتماد على المحددات.
- وبسبب التطور العلمي الذي لحق بعلم الرياضيات ومع ظهور النظريات، قام العلماء بتقديم العديد من الإثباتات بأن هذه القاعدة غير دقيقة بنسبة كبيرة، مما جعل العلماء يلجأون إلى الاعتماد على طريقة غاوس.
- تقوم القاعدة على التوصل إلى حل المعادلات الخطية من خلال الاستفادة من متغير واحد فقط.
- كما تهدف إلى التوصل لحل المعادلة من خلال الاعتماد على حل واحد أو بمجموعة من الحلول التي لا يكون لها حل.
- ولكي يتم التوصل لهذه النتيجة لابد من التوصل إلى القيمة الحقيقية والتي تتمتع بدقة عالية لمصفوفة المعاملات.
- ويقوم الباحث بالتوصل إلى النتيجة تبعاً للرقم النهائي، فإذا كان العدد النهائي يساوي صفر، فهذا دليل على أن المعادلة الجبرية يكون لها عدد لا حصر له من الحلول، أو قد لا يكون لها حلول إطلاقاً، وفي حالة أنها لا تساوي صفر فهذا يدل على وجود حل واحد لها.
المنحنيات الجبرية
- يشكل منحنى المستوى الجبري الذري في علم الرياضيات مجموعة صفرية في مجموعة من الحدود واثنين من المتغيرات.
- منحنى المستوى الجبري الإسقاطي فهو عبارة عن الصفر المحدد بمستوى إسقاطي متنوع الحدود، كما أنها تكون متجانسة ومتشابهة في ثلاث متغيرات.
- ومن الممكن أن يتم استكمال منحنى المستوى الجبري للطائرة في منحنى المستوى الجبري الإسقاطي وهذا عن طريق تشابه مجموعة من الحدود المحدد له.
- وقد يتوقف منحنى المستوى الجبري الإسقاطي على المنحنى الخاص بالمستوى الجبري الأفقي عن طريق القيام بتبديل واحد غير محدد لعدد من الحدود المتجانسة المحددة.
- ولكن هاتين العمليتين يكونا عكس بعضهما البعض، ففي بعض الأحيان يتم استخدام منحنى المستوى الجبري بدون القيام بتحديد إذا كانت الحالة الجبرية أو الحالة الإسقاطية محل النظر.
- فالمنحنى الجبري عبارة عن مجموعة جبرية لها بعد واحد متساوي.
- كما يمثل مجموعة جبرية تتساوى مع المستوى الثنائي منحنى مستوى جبري.
- وفي حالة وجود المنحنى بمساحة تابعة، فيكون بإمكان الفرد أن يقوم بأخذ إسقاط لهذا التكافؤ الثنائي.
- بحيث يسمح لمعادلات التكافؤ بالتقليل من هذه الدراسة الخاصة بالمنحنيات الجبرية، حتى يتم القيام بدراسة منحنى المستوى الجبري.
- وهذا بالإضافة إلى أنه لن يتم المحافظة على عدد من الخصائص تحت معادلة birational، ويشترط دراستها على شكل منحنيات غير مستوية، وغالباً تعرف باسم منحنيات الفضاء أو منحنيات الانحراف.
- ولكن على وجه خاص يعرف المنحنى الجبري بأنه ناعم، بسبب أن الكثير من منحنيات الجبر الغير مفردة لا تكون متساوية مع أي منحنى مستوى جبري.
المنحنى الجبري بالهندسة الإقليدية
- هو عبارة عن مجموعة من النقاط والتي تكون إحداثياتها عبارة عن حلول كثيرة الحدود ثنائية المتغير.
- وفي بعض الأحيان تعرف هذه المعادلة باسم المعادلة الضمنية للمنحنى، على النقيض لمنحنيات الرسم البياني.
- وفي حالة وجود منحنى معطى من خلال هذه المعادلة الضمنية، تكون المشكلة الأولى عبارة عن تحديد شكل المنحنى وطريقة الرسم، وأنه صعب حل هذه المشكلات مثلما في الرسم البياني لأي دالة.
- فمن الممكن أن يتم حساب القيمة y بشكل سهل لقيم متعددة من x.
- فالمعادلة المحددة هي عبارة عن حدود متعددة يقصد بها أن المنحنى يوجد له بعض الخصائص الهيكلية التي من شأنها تساهم في علاج هذه المشاكل.
- من الممكن أن يتم تحليل كل منحنى جبري بطريقة مختلفة ومتميزة إلى عدد معين من أقواس الرتابة الناعمة وتعرف أيضاً باسم الفروع.
- وفي بعض الأحيان تكون مرتبطة بعدد من النقاط التي تعرف باسم نقاط ملحوظة، وقد تكون عدد معين من النقاط المعزولة التي تعرف باسم الأمواد.
- ويسمى قوس رتابة أملس بالرسم البياني التابع لوظيفة ناعمة، حيث يمكن تعريفها على فاصل مفتوح للمحور س في مختلف الاتجاهات.
- فالقوس هنا يكون غير معرف، حيث يعرف باسم القوس اللانهائي، وقد يكون له نقطة نهاية سواء كانت نقطة فردية أو نقطة موازية لأي محاور الإحداثيات.
تعريف المحددات
هي عبارة عن نظرية علمية جديدة تتم من خلال التوصل إلى حلول خاصة بالمسائل الرياضية والمعادلات الجبرية بشكل سلس وسهل، وهذا من خلال القيام بتنظيم بعض العناصر بطريقة منظمة بمريع فيه تقسيمات وتكون عبارة عن صفوف وأعمدة، وأرقام الأعمدة تكون عبارة عن أرقام الرتب بالمحددات الرياضية.
خصائص المحددات
تتمتع المحددات بمجموعة من الخصائص، وهي كالتالي:
- في حالة إذا كانت العناصر الموجودة بأي صف أو موجودة بأي عمود بالمحددة الرياضية وكانت القيمة الخاصة تساوي صفر بأي محدد آخر، فالقيمة النهائية للمحدد الموجود تساوي صفر.
- وفي حالة تساوي القيمة والإشارة لجميع العناصر المتقابلة بأي صفين أو أي عمودين بالمحددة الرياضية، فهذا يدل على قيمة المحدد سوف تكون صفر.
- أما في حالة تشابه كل العناصر التي تساهم في تكوين المحددة وأصبحت بعد ذلك تساوي صفر، ما عدا العناصر الموجودة على القطر الأساسي للمحددة، ولكي يتم الحصول على القيمة النهائية لهذا المحدد يتم ضرب عناصر القطر الأساسي.
- قيمة المحدد أي محدد تكون متشابهة حتى في حالة استخدام قيمة عناصر صف معين أو قيمة عناصر عمود معين في نفس المحدد.
- وفي نهاية الأمر يكون هناك تشابه في قيمة وإشارة المحدد ولا يحدث لها أي تغير سواء في حالة استخدام عناصر الصفوف أو الأعمدة.
طريقة إيجاد قيمة المحددة
يتم إيجاد قيمة المحددة من الدرجة الثانية، من خلال حاصل ضرب عنصري القطر الأساسي ويتم طرح حاصل ضرب عنصري القطر الثاني، وتعرف محددات المصفوفات من الرتبة 3*3 باسم محددات الدرجة الثالثة، حيث يتم حساب المحددات من هذا النوع من خلال استخدام قاعدة القطر.
وفي نهاية مقالنا نكون قد قدمنا لكم طلابنا الكرام بحث علمي عن قاعدة كرامر ، يسعدنا تلقي استفساراتكم عن طريق التعليقات اسفل الموضوع وسوف يتم الرد عليكم على الفور.